
[From the last episode: We looked at the convolution function that defines the CNNs that are so popular for machine visionTechnology that gives machines the ability to see things and make decisions based on what they see. applications.]
This week we’re going to do some more math, although, in this case, it won’t be as obscure and bizarre as convolution – and yet we will find some commonality. If you’re a whiz at matrix math, then you can probably skip most of this, although the conclusion at the end is important (in case it’s not already obvious to you).
We’re going to talk about multiplying matricesAn array of numbers, having both rows and columns of numbers. Widely used for many complex tasks.. Why? Because, in today’s ANNsA type of neural network that’s loosely inspired by biological neurons, but operates very differently., we represent everything in matrices. Within each node, the “kernel” is a matrix of weights, and we multiply an input matrix by that kernel.
So how does that work? Let’s do an easy example. If you’re not familiar with matrices, they’re arrays of numbers having some number of rows and some number of columns. (A matrix like that is 2D. You can have 3D or even higher dimensions; those are called “tensors,” but the notions remain the same.)
Let’s start with two simple 3×3 matrices that we will multiply together. You can’t just multiply any two random matrices, but by working with square matrices like this, we don’t have to worry about that detail.
A Matrix Multiplication Example
The two matrices are:

To do this, we do an odd thing: we start by going across the first row of the first matrix and the first column of the second matrix. As we go to each number in the row and column, we multiply those numbers, and then we add all of those results from the first row and column together to get the first cell of our product.
So, we take 1×2 + -3×0 + 9×0 and that gives us a total of 2. So 2 will be the first cell of our result.
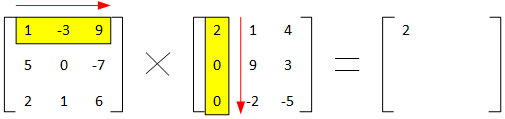
We then stay with the first row, but move to the second column of the second matrix and do the same thing. This time, our result is 1×1 + -3×9 + 9x-2 giving -44. We put this in the top row, middle column of the result (since we used the top row and middle column in the two starting matrices).
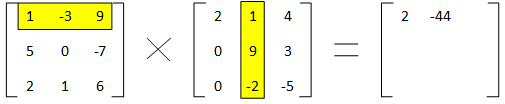
We finish the top row of the result by moving to the last column of the second matrix. Here we get 1×4 + -3×3 + 9x-5, yielding -50.
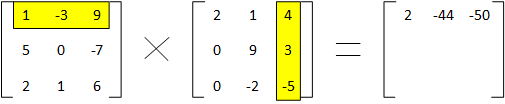
We’ll do one more and then I think you’ll see the pattern. Having completed the top row, we move to the second row of the first matrix, and we restart with the first column of the second matrix. Now we calculate 5×2 + 0x0 + -7×0 for a total of 10, and we add that to the result matrix.
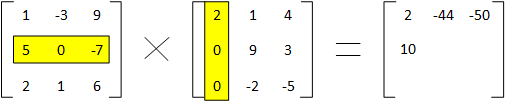
From here, you should be able to finish up the rest of the answer:

So What?
So why did we go through all of this? Well, you probably noticed that we got our result by multiplying a bunch of pairs of numbers and then adding the results together. And, in fact, we did that last week with the convolution as well.
There are a couple of names for what we’re doing. A more formal one is “sum of products”: we take a bunch of products and then we sum them together. But a more common name these days is “multiply-accumulate”: you do lots of multiplication, accumulating the results together as you go. Multiply-accumulate is often abbreviated as MAC. If you’re anywhere around engineers building this stuff, you won’t have to wait long until you hear something about how many MAC resources they’ve put in the thing, for instance.
This kind of math has driven the kinds of hardwareIn this context, "hardware" refers to functions in an IoT device that are built into a silicon chip or some other dedicated component. It's distinct from "software," which refers to instructions running on a processor. that are best at running these machine-learning (MLMachine learning (or ML) is a process by which machines can be trained to perform tasks that required humans before. It's based on analysis of lots of data, and it might affect how some IoT devices work.) calculations. Graphics processing units – GPUsA processor optimized for rendering images and video on a display., the things in your laptop that handle the graphics for your display – have tons of MAC units, and that’s why they’ve been much more successful at doing ML than regular processorsA computer chip that does computing work for a computer. It may do general work (like in your home computer) or it may do specialized work (like some of the processors in your smartphone). have been. And new kinds of processors are being developed specifically for ML. They may not be organized quite like a GPU, but, one way or another, they’ve got to be really good at doing MAC math.

Leave a Reply