
[From the last episode: We looked at some fundamental electrical concepts, with a focus on Ohm’s Law.]
Having looked at Ohm’s Law, we’re now going to veer in a completely different direction. But not to worry: we’ll bring it all back together in a couple weeks. Before we can do that, we need to look at some of the important elements of a memory. We have two building blocks to talk about today.
Let’s start by remembering that, with a memory, you give it an addressWhen referring to memory, a binary number that shows where, within some memory block, the data you want is located. If you want to read or change that data, you have to give the address so that the right data is read or changed., and it tells you what the contents of that address are. (Same thing happens when writing to a memory, only, instead of looking at the contents, you change the contents. But we won’t worry about that.)
With this in mind, we need to ask two questions: how can an address take us to a specific memory location, and how can we tell what the contents are once we have selected that location?
Decoding
We answer the first question by looking into a digital logic block called a decoder. The point of an address is to select something – in this case, a memory cell. We do this by encoding the address in some way. There are a variety of ways to do that, but we’ll take the simplest: a simple binaryA base-2 counting system (rather than the base-10 system we usually use). Digits can be 0 or 1. address. This lets us use an address of some length to select one of many different possibilities. The number of possibilities is determined by the length of the address.
If the address is only one bit long, then we have two choices: the selection when that bit is 0 and the selection when that bit is 1. There are no other possibilities (remember that this is digital, so there is nothing between the 0 and 1). We can illustrate this in a couple of ways. And… in doing this, we run into the issue of engineers counting differently from the rest of us.
Engineers count starting from 0. So the first four numbers would be 0, 1, 2, and 3. As we’ll see, this makes good sense from the standpoint of an address. But… just to keep it a bit real, I’m going to number the “things” we’re selecting starting with 1 as the “first” thing. (Starting with 0 as the “first” thing may be technically more accurate, but it’s weird saying “0 is first and 1 is second, etc.”).
A 1:2 Decoder
So we can represent how a decoder works using a table like this:
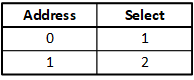
We interpret this in a pretty straightforward way: when the address is 0, select the first thing. When the address is 1, select the second thing. We need only one bit to represent this address – which would correspond to one “line” in a circuit. That line can take on the 0 or 1 values (which might physically mean that they can be LOW for 0 and HIGH for 1, with low and high referring to the voltageVoltage is what gets electrons to flow. It's analogous to water pressure, which gets water to flow. Voltage is measured in units of "volts."). So we can depict this decoder in the following block diagram:
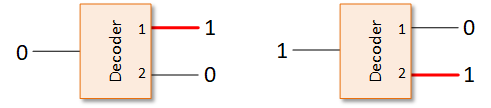
The “1” and the red lines on the outputs indicate which of the options we’ve selected. (The “1” and “2” labels inside the box usually aren’t shown; I do it here just to make it easier to follow what’s going on.) We refer to this as a 1-to-2 (sometimes written 1:2) decoder because we take one bit to select from two choices. Or we just call it a one-bit decoder.
A 2:4 Decoder
We can add another bit to the address, which will let us select from more than two options. With two bitsThe smallest unit of information. It is a shortened form of "binary digit." Since it's binary, it can have only two values -- typically 0 and 1., you can select from four options in a 2:4 (“two-to-four”) decoder.
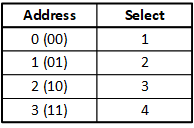
The block diagram for this would look like:
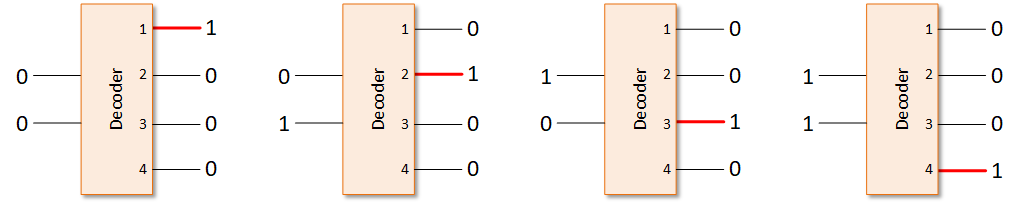
There’s a really good, simple question that you could ask right now: what are we selecting? And that would depend on what we’re doing with this decoder. Decoders can be used for anything where we need to make a selection. It could select, say, which output we send something out on. Or we could select which of a series of alarms or alerts to activate. In our case, we’re going to use it to select a part of a memory. But we’ll do that in a couple of weeks.
Detecting the Outputs
We’re going to leave decoders completely behind for now and look at another piece of a memory: what’s called a sense amplifier, or sense amp. This circuit isn’t as general as a decoder. While decoders can be used all over the place, this one is pretty much limited to use in a memory.
Also unlike a decoder, this is an analog circuit, not a digital one. Its result can – and usually is – turned into a digital answer, but it doesn’t have to be. And that’s going to be important for what we look at in the future.
A sense amp basically tells us whether or not currentThe amount of electrical flow. Measured in amperes or amps (A). is flowing through it. Or whether there is a large amount of current or a small amount of current. That’s the “sense” part. And it’s usually measuring very small current differences, and it has to amplify those differences to give a meaningful output – hence the “amp” part.
If it’s a large amount of current, then, for a digital version, we might turn that into a “1”. If it’s a small amount, we might turn that into a “0”. If we wanted to do this in an analog fashion, then we could use the sense amp to tell us specifically how much current is flowing. In other words, not just “lots” or “a little,” but (making numbers up here) anything from 1 – 100 µA (that’s “microamps,” or a millionth of an amp).
As a hint to what we’re going to talk about in a couple of weeks, we combine decoders and sense amps so that, first we select something, and then we see if there’s current as a result. But I’m getting ahead of things here. We’ll stop here for now.

Leave a Reply