[From the last episode: we reviewed and summarized our discussions over the last few months.]

OK, so we’re back on track with sensorsA device that can measure something about its environment. Examples are movement, light, color, moisture, pressure, and many more.. And, specifically, we’ve been looking at motion sensors, starting with accelerometers. But we’re done with those (for now); we move next to a necessary companion to the accelerometer: the gyroscope. AccelerometersA sensor that measures acceleration and deceleration. measure motion in a straight line; gyroscopesA sensor that detects when it changes direction. measure rotation acceleration.

One of the more natural ways to think of rotation is how it applies to you when you’re driving a car. With cars, we get both straight lines and curves, and so, if we want to know everything about how we move, we need more than just an accelerometer to measure it.

Shifting or Rotating?

But it’s easy to confuse linear motion with rotation. For instance, let’s say you’re on a road that has a straight section, and then it turns to the left. You’re going at a constant speed forward, so there’s no acceleration in that direction. (In fact, the only acceleration then is the effect of gravity attempting to accelerate you downwards.)

Now… if you start moving to the left, courtesy of the curve in the road, then you’re going to feel some acceleration towards the left, since now you’re moving a little bit in a left-right direction while you weren’t before. If you think of your motion as going from totally forward – let’s say north – to NNW, well, after that change, you’re still going mostly north (although less than you were going before), but you’re also going a little bit west. The only way to change speeds (from, say, zero towards the west to a little bitThe smallest unit of information. It is a shortened form of "binary digit." Since it's binary, it can have only two values -- typically 0 and 1. towards the west) is by accelerating (or decelerating), so you must have decelerated a little in the northerly direction, but accelerated a little in the westerly direction.

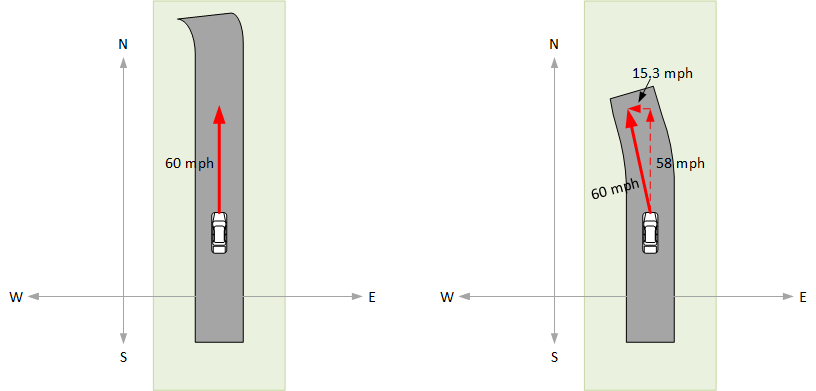
If your speedometer says you’re going a constant speed – say, 60 mph (or kph, as you might prefer) – then you change from 60 mph all north to something a little less than 60 mph north and a slowish speed west. Mechanical engineers and physicists describe this using so-called vectors, which they depict as arrows pointing in a certain direction. It looks nerdy, but, if you look at the different pieces in the following drawing, it can make sense. Pythagoras says that if you’re going 60 mph at towards the NNW and 58 mph north, then you must be going a tad over 15 mph towards the west. (Sorry for that foray into geometry…)

Are You Facing the Same Way?

But there’s a critical thing here: you may have changed from going straight forward to moving at an angle, but did you rotate? Look at two different ways of doing this curve:

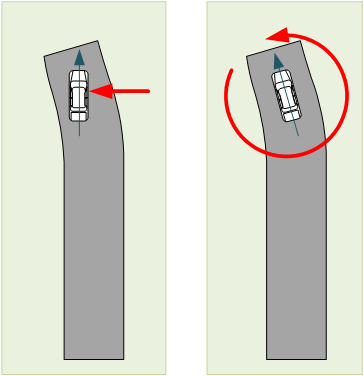
See the difference? In the one on the left, the car has moved into the turn – but it’s still facing forward. That’s not what the wheels usually let a car do, so the only way this could happen is if the car skids to the left – say it was hit by a big gust of wind from the right on a slippery roadway.

The second image shows something that looks more natural: the car is still facing in the direction of travel. So, not only has the car started moving a bit westwards, but it also has rotated a little bit so that it still faces forward.

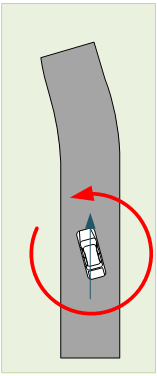
The word we use to describe the direction we’re facing is orientationThe direction someone or something is facing. This may be different from the direction of motion.. You can change your direction of travel, and you can change your orientation. They’re two separate things. Above on the left, we see a change in direction with no change in orientation. We could also have the car moving in a straight line, without changing direction, and, if something weird happened – like a different odd gust of wind – the car could end up spinning and, if the roadway were slick, still keep moving forward.

Freedom to Move and Rotate

There is a key here: the car wants to keep moving in whatever direction it’s already moving. That’s inertiaThe tendency for an object to keep moving (or not moving) at a constant speed if you don’t accelerate or decelerate it. There’s inertia in a straight line and there’s also inertia of rotation – spinning things want to keep rotating in a specific direction unless you force them to change.. So in that last scary scenario, even though the car rotated a little bit (or even a lot), the car still wants to keep moving forward, the way it was already going. Because the road is slick, there’s not enough traction, and the car keeps going in the same direction – except that now it’s facing a different way. I don’t recommend you try this at home. Or on the highway.

It’s the same way with rotation: once rotating, nature wants you to keep rotating the same way. Instead of regular momentum, this is called angular momentum. If you’re not spinning, you tend to stay not spinning – unless you accelerate your rotation and start spinning. If you’re already spinning, then you have to accelerate or decelerate the spin to change how fast you’re spinning.

This gets us back to that whole degrees-of-freedom discussion. We have directions we can move – three degrees of freedomA setting or property that can be adjusted independently without affecting any other setting. With movement, there are three straight-line degrees of freedom: forward/backward, up/down, and left/right. – and we have directions we can face – three more degrees of freedom.  We have accelerometers that measure the movement speed change, but that accelerometer won’t measure any rotation that changes our orientation.

And that’s what gyroscopes are for. It’s the rotational sibling of the straight-line accelerometer. Next time, we’ll look at how gyroscopes work.