In-Memory Computing

[From the last episode: We saw how a resistive memory cell can perform multiplication]

We can now complete the picture of how we can use a memory for AIA broad term for technology that acts more human-like than a typical machine, especially when it comes to "thinking." Machine learning is one approach to AI.. As we saw, AI involves lots of sums of products, also known as multiply-accumulates. Multiply a bunch of pairs of numbers and then add the results together.

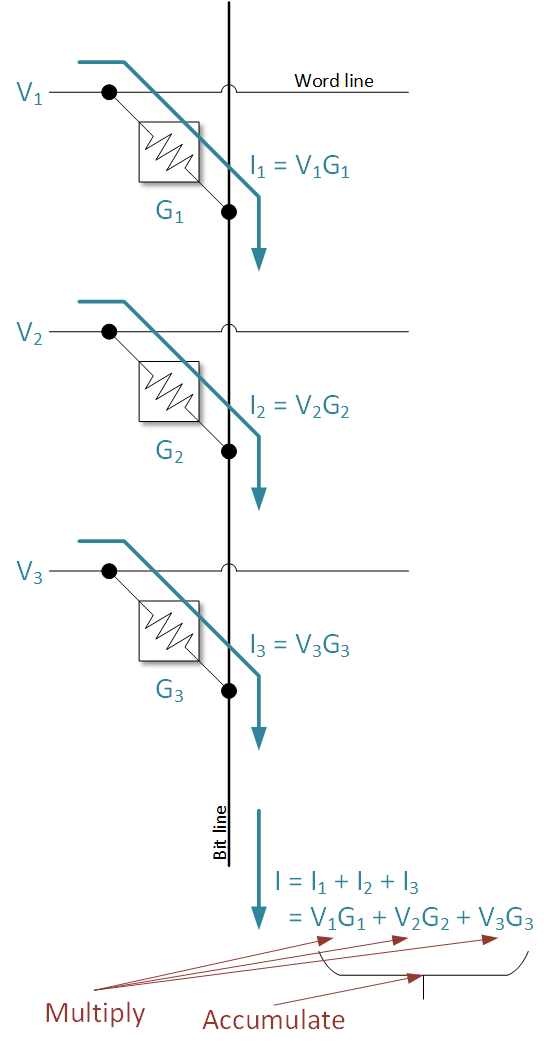
Well, we can now modify a memory so that it can do this. We saw that by programming a very specific value into a memory cell (not just 0 or 1) and by setting a very specific voltageVoltage is what gets electrons to flow. It's analogous to water pressure, which gets water to flow. Voltage is measured in units of "volts." on the word lineA line in a memory that selects which word (and its associated bit cells) will be selected for reading or writing, based on the memory address. The word lines and bit lines are orthogonal to each other, making an array of the bit cells that connect them. (not just “high”), we can perform multiplication of the word-line voltage and the bit-cell conductanceThe literal opposite of resistance. Rather than how hard is it to push the flow through, it looks at how easy it is. Measured in mhos.. The product is the currentThe amount of electrical flow. Measured in amperes or amps (A).. By measuring that current, we learn the result of the multiplication.

But there’s one more change we need to make to our traditional memory in order to make this work. In a normal memory, only one word line goes high at a time. The address determines which word line that will be. We’re going to do something different here. We’re going to let more than one word line go to… some voltage at the same time. (We’ll deal with the decoder question later…)

So now we can have more than one bit cell doing multiplication along the same bit line. Remember that the bit line senses the current? Well, now it’s going to be sensing not only the current from one bit cell, but from any number of them that happen to be doing multiplication – which could be all of them.

And each of those bit cellsA cell that stores a single bit within a memory. (Some can store more than one bit.) It connects a word line to a bit line. The bit cell can either conduct or not conduct current; those are the two states of the memory cell., by doing multiplication, creates a current. And each of those currents goes onto the bit line. So now the sensing on the bit line is measuring the total of all of those currents*. It’s like streams flowing into a river. The total river flow is the accumulation of all of those streams.

What Just Happened?

So let’s back up and see what we have. We have a bunch of multiplications, each of which creates a current. We’ve got a line where all of those currents are added up – that is, it’s a sum. So – here’s the big finish: We have a sum of products. Or we have multiply-accumulate. We’re doing math without math circuits; we’re doing it within a modified memory.

This capability is called in-memory compute, or sometimes compute-in-memory. (Everyone has their preferred phrasing.) The circuits to do the math the traditional way would be quite large; each of these bit cells is much smaller.

So can we just throw out our traditional multiply-accumulate (MAC) circuits and replace them with these memories? Not quite. Let’s review why this is useful, and where it will and won’t help.

Yes, math circuits can be large. But, as we’ll see, some of the other things we need for this will make the memory larger as well. So it’s not just about the size of the circuits.

Where’s My Dang Data?

One of the biggest challenges for AI is the fact that, before we can do all the multiply=accumulate, we need to get the data for that computation from somewhere in memory. That happens a lot, so there’s lots of data movement. In fact, it can become the bottleneck. And, worse yet, moving all of that data requires lots of powerThe rate of energy consumption. For electricity, it’s measured in watts (W).. It can be one of the biggest power hogs in the systemThis is a very generic term for any collection of components that, all together, can do something. Systems can be built from subsystems. Examples are your cell phone; your computer; the radio in your car; anything that seems like a "whole.".

So what would happen if we tried to replace standard math circuits with memories everywhere? Well, for the most general usage, you’d still have to move all of that data – and then you’d have to program the resistanceForces that tend to reduce the amount of flow or current. Measured in ohms (Ω). values into the memory. That would take a super long time, and we didn’t save anything because we’re still moving data.

No, this helps in one important way. And we need to make an important distinction to understand it. Many of the computations we do involve numbers that come as part of some prior computation. We’re using some results to do further calculation. We’re not going to know those results ahead of time; we learn them as we go. And typically, as we learn them, we store them away and then bring them back later.

A Weighty Matter

But there’s one important thing that we do know from the very start: those weights that we need to multiply by other values. Those weights are a permanent part of the AI model. Those numbers are known before we even turn the power on.

So if we can create a bunch of smallish memories for all of the different weight calculations, then we can program the weights into the bit cells – and just leave them there. We don’t know the numbers we’ll have to multiply them by ahead of time, but that’s ok: we’ll put those numbers on the word lines. We don’t have to program them in.

And, better yet, the kinds of memory cells we’ve been talking about hold their contents even with the power off. So we could literally program in the weights as part of the manufacturing process. We’d then never need to program them again (unless we updated the system with a new and improved model, and then we’d program that update in just once).

So we’ll still need to move some data around, but not the weights. And that’s a significant savings. If we can implement this idea in a robust fashion, then we’ve saved a significant amount of power.

But there are still some things we need to add to the memory to make this work, and this means understanding some other fundamental circuits. We’ll look at that next week. And then we’ll look further at the caveats.

 

*Note: for those of you not so into the math that’s used in engineering and science, the number subscripts simply let us look at different examples of the same thing. So V₁ is a voltage in one place – call it Place 1. V₂ is the equivalent voltage someplace else – Place 2. So all those subscripts show that we’re doing the same thing with each of the 3 products, but that each cell has its own V, G, and resulting I.