
[From the last episode: We looked at two important circuits: decoders and sense amplifiers]
We’re building up to an interesting machine-learning technique, but we’re having to set lots of groundwork first. We saw Ohm’s Law two weeks ago, and we looked at decoders and sense amps last week. We’ll come back to them eventually; for now, we’re going to look at some memory basics.
We won’t get into huge detail, but memory structure will be important for understanding the MLMachine learning (or ML) is a process by which machines can be trained to perform tasks that required humans before. It's based on analysis of lots of data, and it might affect how some IoT devices work. concept that’s coming up. I’ve struggled a bit to figure out how best to explain this, so bear with me. It’s not super complex, but I find that, if I’m not careful, I could end up tying everyone in knots. So… here goes.
Rows and Columns
When we think about a memory, we often think about providing an addressWhen referring to memory, a binary number that shows where, within some memory block, the data you want is located. If you want to read or change that data, you have to give the address so that the right data is read or changed. and getting a result, and that’s indeed what happens – sort of. The thing is, even though the address can take us to a specific bit in memory, we usually don’t get one bit at a time. At the very least, we’re getting a byteA byte is 8 bits. – that is, 8 bitsThe smallest unit of information. It is a shortened form of "binary digit." Since it's binary, it can have only two values -- typically 0 and 1.. We might be getting as much as 32 or even 64 bits at a time.
That means we’re not really addressing a bit at a time; we’re addressing a byte or a word at a time. So how does that work? Let’s first look at how the memory is organized to help this all make sense.
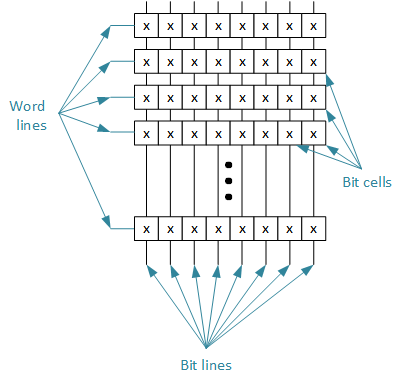
A memory is an array of what we call bit cellsA cell that stores a single bit within a memory. (Some can store more than one bit.) It connects a word line to a bit line. The bit cell can either conduct or not conduct current; those are the two states of the memory cell., and each bit cell stores a single bit. (There are technologies where a bit cell can store more than one bit, but we’re not going to talk about that now.) In this example, we’ll be getting a byte, or 8 bits, at a time, so we organize the memory in rows of bytes. Then we select a row to find out what’s stored on its particular 8 bits.
In this approach, the rows are called word lines, and the columns are called bit lines. I’ve put “x” in the bit cells just to show that they could be 1 or 0 for a normal memory.
Addressing a Row
If we want to access something in this memory, the first thing we want is to select a row, and then that row will show up at the output – all 8 bits. If we start with a 16-bit address, then we have to adjust the address to take into account that we’re trying to select one row of 8 bits, not one individual bit.
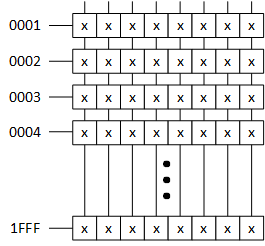
We do this by separating the address into two portions: 3 bits get us to one of the output bits (since 3 bits let us count to 8); we use the remaining 13 bits to select the word lineA line in a memory that selects which word (and its associated bit cells) will be selected for reading or writing, based on the memory address. The word lines and bit lines are orthogonal to each other, making an array of the bit cells that connect them.. By conventionAn agreement on some decision that could be made several ways. For example, given a single bit, you could decide that 1 means "true" and 0 means "false," or you could decide the opposite. Similar in spirit to a protocol, but protocols usually deal with how something is done -- a step-by-step process, for example., we use the 3 bits on the right of the address to select one of the bit lines (if we wish), and we use the leftmost 13 bits to select the word line. That means that we will have 1FFF rows (using hexadecimal numbers), which is the biggest number we can make with 13 bits (1FFF is the same as 1 1111 1111 1111).
So we can number the rows as shown below.
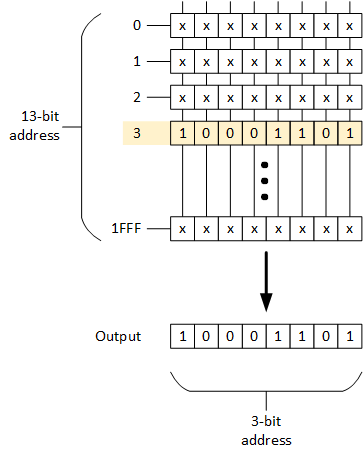
Now… let’s say that row 3 has the value 10001101 stored in it. We take the leftmost 13 address bits (16 minus the 3) and we address the row with 0003 (0 0000 0000 0011) since we’re going for row 3.
By selecting row 3, we get its value at the output. (I’ve left the rest of the memory with “x” simply because I don’t care about them. They’ll have some values of their own.)
We Have Part of a Memory
So let’s quick review: we took a 16-bit address and we split it up so that 13 of the bits could select a row and then, once we have that output, if we wanted to, we could select one of the 8 output bits with the remaining 3 bits of the address (we’ll deal with this later). This is conceptually how we organize memories. Next week, we’ll add a couple more pieces to this puzzle so that we can make a real memory. And it will all become clearer, if it’s not clear already.

Leave a Reply