Hexadecimal: Counting by 16

[From the last episode: We looked at different categories of processor]

We’re going to look at big and little microprocessorsA computer chip that does computing work for a computer. It may do general work (like in your home computer) or it may do specialized work (like some of the processors in your smartphone)., but before we do that, it’s helpful to understand how engineers count so that we can discuss memory addresses more easily. It’s hard for me to know how obvious this whole thing will be, but I’m pretty sure that it won’t be for folks that haven’t spent a lot of time with math. So if you already understand number counting systemsThis is a very generic term for any collection of components that, all together, can do something. Systems can be built from subsystems. Examples are your cell phone; your computer; the radio in your car; anything that seems like a "whole.", then this will be very much a review. I go into some detail for anyone that’s new to these ideas.

Because everything in computers is binaryA base-2 counting system (rather than the base-10 system we usually use). Digits can be 0 or 1. – 0s and 1s – our normal decimalThe base-10 counting system that we usually use. Digits can go from 0 to 9. numbers aren’t very convenient, for reasons we’ll see in a sec. So instead, we work with so-called hexadecimalA base-16 counting system (rather than the base-10 system we usually use). Digits can go from 0 to 9 and then A, B, C, D, E, and F. numbers (or hex for short). That’s base-16 counting, instead of our base-10 (decimal) counting. That works better for binary numbers since 16 is a power of 2, while 10 isn’t. This gets clearer if we look at the bitsThe smallest unit of information. It is a shortened form of "binary digit." Since it's binary, it can have only two values -- typically 0 and 1. that make up, say, an addressWhen referring to memory, a binary number that shows where, within some memory block, the data you want is located. If you want to read or change that data, you have to give the address so that the right data is read or changed.. (Note that there’s yet another engineering way of counting – by 8, called octalA base-8 counting system (rather than the base-10 system we usually use). Digits can go from 0 to 7.. The concepts are basically the same, and hex is more applicable for us, so we won’t go into detail on that.)

If we’re going have an address that can go from 0 to 15, then we need 4 bits:

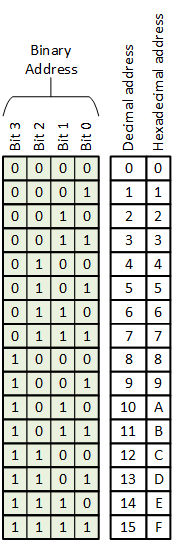
What we’re doing here is taking a binary number, shown as bits 0, 1, 2, and 3, and writing them as something easier to understand than just 1s and 0s. But you can see the natural binary sequence, starting with all 0s and filling in 1s until we’re done filling 1s.

What We Do with Decimal

If you haven’t thought hard about our counting system, this may be confusing. So, at the risk of being overly simple, let’s review how we normally count using decimal numbers. We have digits, and each digit is some number between 0 and 9. Once we get to 9, we need a new digit to count higher – and we restart the first digit.

Let’s look at a simple example. In reality, there is already a second (or more) digit; we just don’t show it if it’s 0. So let’s deal with two digits. The number “0” (as we’d normally write it) is the same as “00.” The number “5” is the same as “05”.

So what we do is start with the smallest digit and go from 0 to 9. To go higher than that, we bump the next digit up by 1 and restart with the smallest digit. So after “09” (which we’d normally just write as “9”), we bump the next digit from 0 to 1 and we start over on the right. That gives us 10. Which is what we expect: 9 is followed by 10.

The Same Thing in Binary

It’s the same thing with binary, except that we have only 0s and 1s; there is no 2 through 9. So, after a digit goes from 0 to 1, well, that digit is now full, so we bump the next digit by 1 and restart with 0 on the smallest digit. We run out of space pretty quickly, so let’s use 4 binary digits, like the picture above. At 0000, the next number bumps the smallest digit to 1 for 0001. Now that smallest digit is as high as it can go, at 1. So to go one more, we need to bump the next digit from 0 to 1 and then restart with 0 on the smallest digit. So we go from 0001 to 0010.

Add one more and you have 0011. Now what happens if we want to add yet one more? Well, we bump the next digit – but that’s already at 1, so we can’t bump it higher. Instead we go to the digit next to that and bump it, and restart with 0 on both of the first two digits. So 0011 goes to 0100. That third digit is now a 1, and the two digits that were “full” at 1 get reset to 0.

Doing That in Hex vs. Decimal

So look back up at that table. You can see that, with the decimal number, we go from one digit to two – 9 to 10 – at a weird place in the binary sequence, not where we’re at some nice, natural place where we’ve filled all the bits. With hexadecimal, we don’t add another digit until after all of the individual bits are full, or “1”. Of course, we don’t have numerals bigger than 9, so engineers use the first five letters of the alphabet (usually, but not always, in capital letters) for those higher digit values. The next number higher than 9 isn’t 10; it’s A. I know, weird, but it works.

To show that more clearly, let’s look at what happens if we want to go one number higher than what we have in the table. Problem is, that would take more bits than the four we showed. With only 4 bits, the highest number we can have is F, or 15. If we want a higher number, we need more bits – and they fill up just like the ones above. So let’s say we have 8 bits instead of 4 (we often keep theses sizes to natural powers of 2). Then the highest number in that table above would be, instead of 1111, or F, 00001111, or 0F. Then next higher number would be 00010000, or 10 in hex. (In decimal, that’s 16.) We bumped the next digit (the 5^th one) and reset the others to 0. And that’s a very natural place to add a new hex digit – much better than the kind-of-random place where 9 goes to 10 in decimal.

Time for a Breath

If this is really new and maybe a little confusing, there’s no need to understand this in detail – there’s no quiz at the end. But when we start looking at processor-related sizes, it makes more sense to talk in hex than in decimal. You can do it either way, it’s just that decimal gets awkward whereas hex, as unnatural as it might look if you’re not used to it, works more smoothly. So if you see things that look like they should be numbers, but they have the letters A-F in them, now you know why.