
[From the last episode: We noted that some inventions, like in-memory compute, aren’t intuitive, being driven instead by the math.]
We have one more addition to add to our in-memory compute systemThis is a very generic term for any collection of components that, all together, can do something. Systems can be built from subsystems. Examples are your cell phone; your computer; the radio in your car; anything that seems like a "whole.". Remember that, when we use a regular memory, what goes in is an addressWhen referring to memory, a binary number that shows where, within some memory block, the data you want is located. If you want to read or change that data, you have to give the address so that the right data is read or changed. – a binaryA base-2 counting system (rather than the base-10 system we usually use). Digits can be 0 or 1. number. In other words, it’s digital. The output of each sense amp gives the contents of a bit cellA cell that stores a single bit within a memory. (Some can store more than one bit.) It connects a word line to a bit line. The bit cell can either conduct or not conduct current; those are the two states of the memory cell.: a 1 or a 0. Again, digital.
But for in-memory computing, we’re putting an arbitrary voltage on the word lineA line in a memory that selects which word (and its associated bit cells) will be selected for reading or writing, based on the memory address. The word lines and bit lines are orthogonal to each other, making an array of the bit cells that connect them., not just making it go high. And we’re trying to measure the specific currentThe amount of electrical flow. Measured in amperes or amps (A). in the sense amp, rather than just saying “yeah there’s some current,” or “No there’s not.”
In other words, we’re going from digital to analog. Memories configured for in-memory compute are often referred to as analog memories.
OK, so that’s all well and good, but what does that mean? Well, most of our system is digital. And yet, at some point, we need to transfer digital information into analog information. Then, when we’re done, we need to take the analog result and convert it back to digital. There are a pair of really important kinds of circuit that we need to look at in order to do this.
Going Analog
Let’s say we want to place a 0.5-V value on a word line. And let’s say that the maximum value on the word line is 1 V. (To be clear, I’m making these numbers up to make things easy.) We know the analog value we want (0.5 V), but what digital value will we be starting with?
That is up to the designer. So let’s say that the designer wanted to use 8 bitsThe smallest unit of information. It is a shortened form of "binary digit." Since it's binary, it can have only two values -- typically 0 and 1. for the digital version of the voltage. 0 volts would be 00 (in hexadecimalA base-16 counting system (rather than the base-10 system we usually use). Digits can go from 0 to 9 and then A, B, C, D, E, and F.); 1 volt (the maximum) would be FF. The easiest thing to do, then would be to have 0.5 V be halfway between: 0F. So, in this scenario, we’ll be starting with a digital number of 0F that we want to transform into an analog value. For this we need a digital-to-analog converter, or DAC.
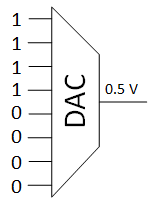
This circuit will literally take the 0F digital number and create 0.5 V on the output. This can then run our word line.
Rounding Off
Notice that, with 8 bits, we can’t represent just any number. We get 256 different values, so we can pick up to that many levels between 0 and 1 V. If we wanted 0.629347 V, there’s no way we could get that. We’d have to round up or down to the closest available number. We can get more precision if we use more bits. Say, instead of 8 bits, use 32 bits. Now we get way more values between 0 and 1 – exactly 4294967296 of them.
But there are always going to be numbers that we can get exactly, no matter how many bits we use. This is sometimes called quantization error or quantization noise. It’s a slight deviation from exact that we get when we use digital representations. It’s the reason, for example, that audiophiles insist that analog records sound better than CDs. (Technically, they’re correct, although it’s a big question as to whether the human ear can notice the difference.)
This becomes really obvious if we use a really small number of bits, like 2. That gives us 4 values, so we can represent (in this example) 0 V, 0.25 V, 0.5 V, 0.75 V, and 1 V.
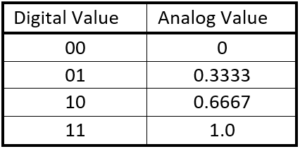
We’ve had to divide up the 1 V into four chunks, including 0. So this is what we end up with. Notice that we can’t represent 0.5 V here! If we want 0.5 V, then we have to choose either 0.3333 or 0.6667 (both of which are themselves rounded slightly, since we know that those decimals go on to infinity).
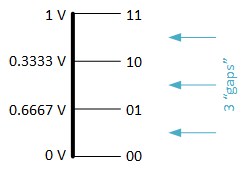
In fact, our getting 0.5 V from 0F is also slightly off. I used that to make it simple, but even though we get 256 values from 8 bits, that means that there are only 255 “gaps” (in the same way that we had only 3 gaps above). That’s… annoying. But, lucky for us, we’re not designing this stuff, so we don’t have worry about it. We just need to know how it works. (Ish.)
Going Back Digital
Once we’ve set all of our word-line voltagesVoltage is what gets electrons to flow. It's analogous to water pressure, which gets water to flow. Voltage is measured in units of "volts." and started driving currents into the sense amps, we’re going to need to transform that analog current value back into a digital number. So we use – wait for it – an analog-to-digital converter, or ADC.
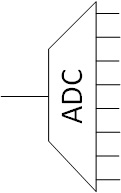
We have the same round-off issue here as we did with a DAC. It’s entirely likely that we won’t be able to represent the measured current exactly in a binary number; we’ll have to round it slightly.
The Complete Picture
We can now add these to what we saw a couple weeks ago, and we have now a complete picture of our in-memory computing structure.
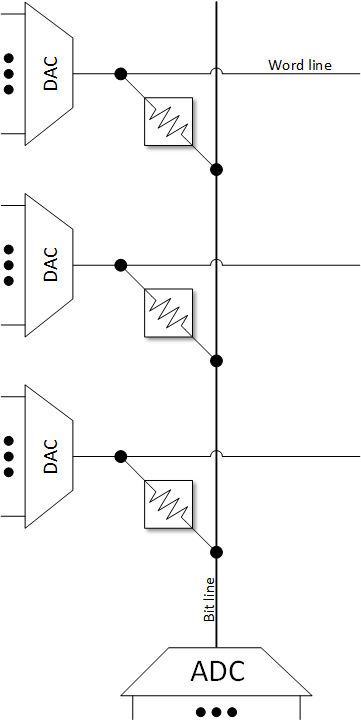
Next week: the promised caveats.

Leave a Reply