[From the last episode: Communications are organized as a stackRelated to communications: A way of organizing parts of a complicated process (like communications) so that any task relies on tasks below it and feeds the tasks above it. Related to computing: A place in memory where you store “where was I?” information when you go from, say, one function into another. Before starting a new function, you store where you were in the old one so that, when the new function ends and you’re back in the old one, you can figure out where you were and continue on., with each layer of the stack providing specific services to the layers above it.]

With the help of stacks, we can understand what’s going on at a high level. But when it comes to detail, there are literally an uncountable number of ways to do things – as many ways as there are to skin a cat. And the only way something is going to work is if everyone agrees on one way. (OK, maybe a very few ways.)

To get us used to this notion, let’s start by taking the most basic of digital electronic entities: the bitThe smallest unit of information. It is a shortened form of "binary digit." Since it's binary, it can have only two values -- typically 0 and 1.. You may know that a bit is a single unit of information that can be 1 or 0. Or “true” or “false.” Or “on” or “off.” The true/false model might make sense for something like a smoke detector: a single bit can tell us whether it has detected smoke (true) or not (false). A thermostat control, on the other hand, feels more natural with a single bit that tells the heater either to turn “on” or “off.”

So far so good. But these are all a matter of interpretation. For some reason, we have a tendency to think of “1” as “true” or “on” and “0” as “false” or “off.” But there’s nothing that says it has to be that way. It’s completely arbitrary.

So at the outset, for a given systemThis is a very generic term for any collection of components that, all together, can do something. Systems can be built from subsystems. Examples are your cell phone; your computer; the radio in your car; anything that seems like a "whole." to work, everyone has to agree as to what “1” and “0” mean.

Deciding on the Meaning of a Bit

At this point, we’re just talking about how we process these ideas in our minds. But in a machineIn our context, a machine is anything that isn't human (or living). That includes electronic equipment like computers and phones., these ideas have to be reduced to physics: electrical or optical signals, most typically. With an electrical line, it’s easiest to control things by using two voltagesVoltage is what gets electrons to flow. It's analogous to water pressure, which gets water to flow. Voltage is measured in units of "volts.". For a long time, integrated circuits worked at 5 volts (abbreviated “V”). So signals had two possible values: a voltage somewhere near 5 V and a voltage somewhere near 0 volts.

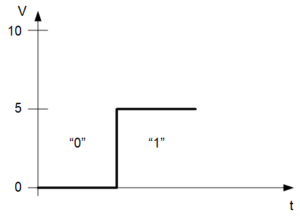
The graph above gives an example of a wire changing from a 0 to a 1. Time moves from left to right along the “t” axis, so the 0 is there first, and then it changes to a 1. The vertical axis shows voltage; it starts at 0 V, and then, at some time, it becomes 5 V. At the other end of this wire, some other equipment will see the 0 V and interpret it as a 0 and then it will see the 5 V and interpret it as a 1.

In this particular example, it shows that the 0-V portion is considered a logic 0, and the 5-V portion is considered a logic 1.

Deciding on How to Implement a Bit

Here again, though, we have a choice. We have a natural tendency to pick 5 volts to be “1” because it’s higher than 0 volts. But imagine that, instead of volts on a line, we have some make-believe system that communicates by color, like an octopus. Let’s say it can take two colors – orange or green. Now, which color is “1” and which is “0”? It really doesn’t matter; there’s no “natural” tendency. You just have to agree that orange is “1” or green is “1” and then stick to that consistently.

It’s the same with voltages on the line. We pick an interpretation and we stick with it. The following figure shows the same graph as above, only with a reversed interpretation of what is 1 and what is 0. And it’s just as legitimate as the one above.

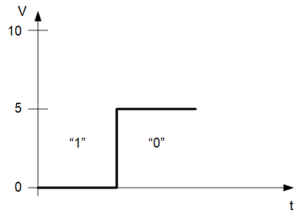
So we’ve just barely gotten started, and already we have all of this complication – and for the absolute simplest possible notion in electronics: the bit. We’ve seen that:

• We can arbitrarily decide what “1” and “0” represent (true or false), and
• We can arbitrarily decide which voltage to use for a “1” and a “0.”

But the only way things can work without complete chaos is if we come to some agreement on how things are going to work. Engineering is full of conventionsAn agreement on some decision that could be made several ways. For example, given a single bit, you could decide that 1 means "true" and 0 means "false," or you could decide the opposite. Similar in spirit to a protocol, but protocols usually deal with how something is done -- a step-by-step process, for example. – decisions made early on so that we don’t get stuck with these arbitrary decisions over and over again. We’re not going to worry about 1s and 0s or volts anymore, but we do need to continue exploring how we agree on such things. We’ll look at that next.