
[From the last episode: We looked at different types of bit cellsA cell that stores a single bit within a memory. (Some can store more than one bit.) It connects a word line to a bit line. The bit cell can either conduct or not conduct current; those are the two states of the memory cell. where resistanceForces that tend to reduce the amount of flow or current. Measured in ohms (Ω). plays a role in how they work.]
We’ve seen how some bit cells are resistive. But, as normally used, they have two “basic” resistances: high and low. Exactly how high or how low is less important – and, for that application, that’s key. Because you want the bit cell to be robust under all kinds of conditions, so you don’t want little variations to mess things up. This is an important theme we’ll return to later.
Separately, we need to harken back to Ohm’s Law, which we talked about a few weeks ago. That law shows how currentThe amount of electrical flow. Measured in amperes or amps (A). is related to voltageVoltage is what gets electrons to flow. It's analogous to water pressure, which gets water to flow. Voltage is measured in units of "volts." and resistance. And we also talked about resistance’s “half-full” counterpart: conductanceThe literal opposite of resistance. Rather than how hard is it to push the flow through, it looks at how easy it is. Measured in mhos.. If resistance is high, conductance is low, and vice versa. Critically, we saw that
I=V*G
where I is current, V is voltage, and G is conductance. Now we’re going to put the two things we’ve seen together.
Bit Cells as Resistors that Multiply
The bit cells we’re talking about act like resistors, which means they have a resistance – which, of course, means that they have a conductance (1 over the resistance). We saw that the bit cell sits between the word lineA line in a memory that selects which word (and its associated bit cells) will be selected for reading or writing, based on the memory address. The word lines and bit lines are orthogonal to each other, making an array of the bit cells that connect them. and the bit lineA line in memory that can detect whether a bit cell conducts current. This is how the memory is read. The bit lines and word lines are orthogonal to each other, making an array of the bit cells that connect them.. So in this case, the V we’re interested in is the voltage difference between the word line and the bit line. That’s what sets the current through the resistor. It’s like the word line is the water tank, and the bit line is the bucket that the water flows into. The hose between them is the resistive bit cell.
Critically, when we use the bit cell as a memory, we say that we select the word line by making it go high. But we never said how high, because, in a memory, that’s a detail handled by the designer, and it kind of doesn’t matter for anyone else – in the same way that the exact resistance doesn’t matter. As long as it goes high, you get current, and as long as you can detect the current, you’re good.
But we’re not going to use this as a memory. So we can’t make all the assumptions that we would make about a memory. Here’s the big takeaway:
Based on the equation above, the exact amount of current we get will be the voltage across the resistor times the conductance of the resistor. In other words, by setting a known voltage on the word line, the current we get results from the multiplication of that voltage times the conductance. The bit cell is doing multiplication!
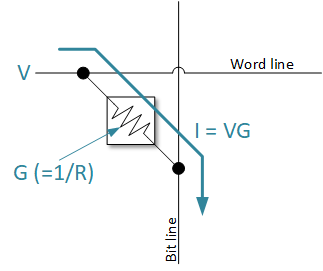
So here’s the thing: if we can set any voltage and set any conductance, then we can multiply any two numbers! As long as we can accurately measure the resulting current; that measurement is the product of the multiplication.
Too Good to be True?
There’s a limit here, of course. There is a reasonable range for the voltage, and there are reasonable limits to the resistance/conductance values we can set. But, within those limits, we have a multiplier – and one that’s way smaller than a standard multiplier circuit.
Are we getting something for free here? Is this too convenient? Are you getting a “what’s wrong with this picture” feeling?
Yes, there are caveats – and significant ones. We’ll talk about them. But the concept is compelling if we can deal appropriately with the caveats.
Resistance Limits
We’ll start with one caveat here: can we put just any old resistance into a bit cell? In principle, the answer is yes – kinda. It depends on the specific type of cell. MRAM cells, for instance, are harder to do this with (but people are trying – or at least, have tried). PCRAM and RRAM cells are probably easier.
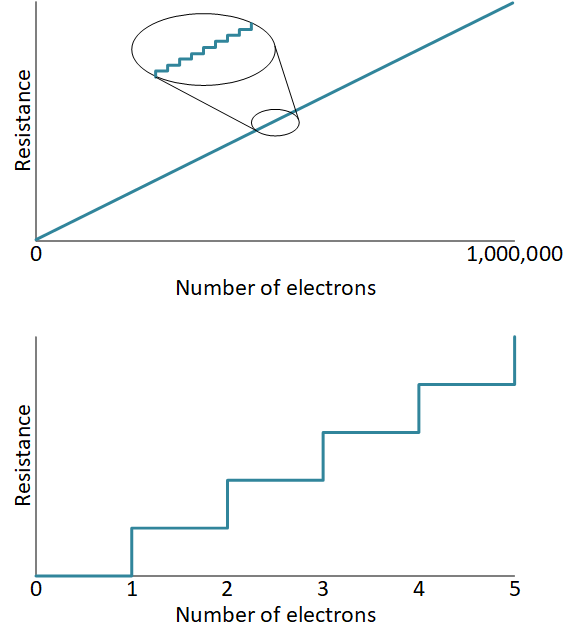
Flash cells have an interesting challenge. The resistance is set based on the number of electronsA fundamental particle found outside atoms. It carries a negative charge. It can move easily in a conducting material, which gives rise to electrical current. captured in that floating gate. Here’s the thing: you can’t capture a partial electron. So you’re going to have some integer number of electrons in the floating gate.
If you have a million electrons, then you have lots of settings available: 1 electron, 2, 3, 4, … all the way to a million electrons. Each one of those gives a different conductance, and so it’s a nice, smooth(ish) knob that you can turn to set the conductance.
But what if you have only, say, 5 electrons? Then you have 6 settings: 0, 1, 2, 3, 4, and 5 electrons. That means only six conductance settings, and you jump from one to the next; there’s no smooth going from one to another. So that places a limit on how many conductance values you can use. You won’t be able to multiply by just any old number; you can multiply only by the numbers available.
Making up numbers here, if the maximum resistance possible were 60 Ω, and if this is linear (we’ll talk more about that later), then your available numbers for multiplying would be 0, 10, 20, 30, 40, 50, and 60 Ω. 36 would not be available; you’d have to round to 40*.
So, no, there is no free lunch. It’s not perfect; there are some gotchas. But let’s complete the picture before we start worrying about that.
* Note: This can’t work physically with those numbers, since you can’t really get to 0 without extreme effort, and the highest number is infinity. So this example serves just to see the effect on the numbers.

Leave a Reply